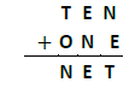Competitive Math Contents
The lessons and problem set for this program are designed to prepare students for various math competitions. The lower level classes prepare and expose students to tackle problems which normally found in Math Olympiad, Math Challenge Tournament and Math Kangaroo. The upper level classes will focus on MathCounts, AMC 8, and Math Olympiad types of problems.
These classes are only available in the summer.
Typical Schedule (Class Format)
Warm-up/Mental Math
Lessons on Topic
Guided Problems
Independent Exercises and Class Discussion
Break
Group/Team Challenge
Group Discussion
Short Problems/Cool Down
No homework except for unfinished classwork
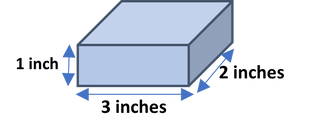
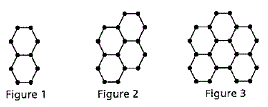
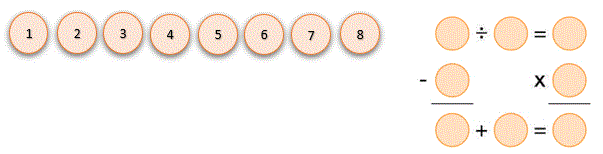
Below is a short description for each level along with sample problems from the curriculum.
These classes are only available in the summer.
Typical Schedule (Class Format)
Warm-up/Mental Math
Lessons on Topic
Guided Problems
Independent Exercises and Class Discussion
Break
Group/Team Challenge
Group Discussion
Short Problems/Cool Down
No homework except for unfinished classwork
Below is a short description for each level along with sample problems from the curriculum.
Introduction to Competitive Math - ENROLL
Contents covered in Track A: Logic and Deductive Reasoning, Algebraic Thinking, Mystery Numbers, Patterns, Orders and Numbers, and Spatial.
Contents covered in Track B: Division and Patterns, Missing Digits and Operation Signs, Alphametics, Arrangements, Organized Lists, and Non-routines.
Sample Problems:
(Orders and Positions) Sal was the 11th person in line for face-painting. Nora was the second from the last person in line. If there were 15 people lined up for the face-painting, how many people were between Sal and Nora?
Contents covered in Track A: Logic and Deductive Reasoning, Algebraic Thinking, Mystery Numbers, Patterns, Orders and Numbers, and Spatial.
Contents covered in Track B: Division and Patterns, Missing Digits and Operation Signs, Alphametics, Arrangements, Organized Lists, and Non-routines.
Sample Problems:
(Orders and Positions) Sal was the 11th person in line for face-painting. Nora was the second from the last person in line. If there were 15 people lined up for the face-painting, how many people were between Sal and Nora?
|
(Spatial) A wooden block is 3 inches long, 2 inches wide, and 1 inch high. The block is painted blue on all six faces. The block is then cut into six 1-inch cubes. How many of the small cubes have only three faces painted blue?
|
|
|
(Alphametics) Given that E = 2, find the value of “TON”.
|
|
Competitive Math 1- ENROLL
Contents covered in Track A: Digits and Numbers, Algebraic Thinking, Patterns, Systematic Listing, Geometry, Logical and Spatial.
Contents covered in Track B: Sequences, Summation, Averages, Number Patterns, Missing Numbers & Palindromes, and Alphametics.
Contents covered in Track A: Digits and Numbers, Algebraic Thinking, Patterns, Systematic Listing, Geometry, Logical and Spatial.
Contents covered in Track B: Sequences, Summation, Averages, Number Patterns, Missing Numbers & Palindromes, and Alphametics.
Sample Problems:
(Pattern) Study the figures in the sequence below. Find the number of dots in Figure 25.
(Pattern) Study the figures in the sequence below. Find the number of dots in Figure 25.
(Missing Numbers) Place the number 1 to 8 into the circles so that the four calculations are correct?
|
(Logical and Spatial) The L-shape pictured is formed from three squares, each 1 cm on a side. Five of these L-shapes are placed next to each other to form a figure. What is the least possible perimeter of the figure they form, in cm?
|
|
Competitive Math 2- ENROLL
Contents covered in Track A: Number Theory (Primes, Composites, Divisibility Rules), Patterns in Calendar, Arithmetic and Averages, Perimeters and Areas, More Geometry (Polygons, Angles, Sum of Angles), and Units Digit.
Contents covered in Track B: Number and Sequence, Rate and Speed, Counting and Probability, Ratios and Fractions, Measurements and Geometry, Algebraic Thinking and Logical Deduction.
Sample Problems:
(Number Theory) A number is a multiple of 9 and it’s larger than 1000. The number is divisible by both 5 and 7, and it is not divisible by 2. If the number is less than 2000, what is the number?
(Counting and Probability) A committee of three is chosen from five counselors - Allen, Benjamin, Coby, Dahlia and Eshita. What is the probability Benjamin is on the committee?
(Measurements) Tom and Dima are designing a fort. They notice that if they increase the length of the floor by 2 feet then the floor area will increase by 12 square feet. If they increase the width by 3 feet, then the floor area will increase by 24 square feet. What are the dimensions of the floor in their design?
Contents covered in Track A: Number Theory (Primes, Composites, Divisibility Rules), Patterns in Calendar, Arithmetic and Averages, Perimeters and Areas, More Geometry (Polygons, Angles, Sum of Angles), and Units Digit.
Contents covered in Track B: Number and Sequence, Rate and Speed, Counting and Probability, Ratios and Fractions, Measurements and Geometry, Algebraic Thinking and Logical Deduction.
Sample Problems:
(Number Theory) A number is a multiple of 9 and it’s larger than 1000. The number is divisible by both 5 and 7, and it is not divisible by 2. If the number is less than 2000, what is the number?
(Counting and Probability) A committee of three is chosen from five counselors - Allen, Benjamin, Coby, Dahlia and Eshita. What is the probability Benjamin is on the committee?
(Measurements) Tom and Dima are designing a fort. They notice that if they increase the length of the floor by 2 feet then the floor area will increase by 12 square feet. If they increase the width by 3 feet, then the floor area will increase by 24 square feet. What are the dimensions of the floor in their design?
Competitive Math 3- ENROLL
Contents covered in Track A: Number Theory, Rate and Proportions, Speed and Movement, Geometry – Polygons and Circles, Counting and Probability, Permutations and Combinations.
Contents covered in Track B: Rates, Ratio and Proportion, Complex Fractions and Percent, Geometry – 3D, Combinatoric - Shapes and Pathways, Statistic and Probability, Number Theory - Mixed Problems.
Sample Problems:
(Number Theory) Abhinav, Bella, and Chandra were all born after 2000. Each of them was born in a year after 2000 that is divisible by exactly one of the prime numbers 2, 3 or 5. Each of these primes is a divisor of one of the birth years. What is the least possible sum of their birth years?
Contents covered in Track A: Number Theory, Rate and Proportions, Speed and Movement, Geometry – Polygons and Circles, Counting and Probability, Permutations and Combinations.
Contents covered in Track B: Rates, Ratio and Proportion, Complex Fractions and Percent, Geometry – 3D, Combinatoric - Shapes and Pathways, Statistic and Probability, Number Theory - Mixed Problems.
Sample Problems:
(Number Theory) Abhinav, Bella, and Chandra were all born after 2000. Each of them was born in a year after 2000 that is divisible by exactly one of the prime numbers 2, 3 or 5. Each of these primes is a divisor of one of the birth years. What is the least possible sum of their birth years?
|
(Geometry) Eight congruent semicircles are drawn inside a square of length 4. What is the area of the nonshaded part of the square?
|
|
(Percent) Mia went shopping to buy a new winter coat. The coat she wanted was on sale for 20%. Mia also gets an additional discount of 10% off the sale price by using her student’s discount card. If Mia pays $180 for the coat, what was the original price before either discount?
(Counting and Probability) A box contains 26 slips of paper, each showing a different letter of the alphabet. If two slips of paper are drawn from the box at the same time, what is the probability that both letters appear in the word ALGEBRA? Express your answer as a common fraction.
(Counting and Probability) A box contains 26 slips of paper, each showing a different letter of the alphabet. If two slips of paper are drawn from the box at the same time, what is the probability that both letters appear in the word ALGEBRA? Express your answer as a common fraction.
Competitive Math 4- ENROLL
Contents covered in Track A: Logic/Reasoning and Number Bases, Number Theory, Geometry – Pythagorean Theorem, Fractions & Exponents, Arithmetics & Data, Counting and Probability.
Contents covered in Track B: Exponents and Radicals, Functions and Operations, Geometry – Areas, Number Bases and Modular Arithmetic, Set Theory and Mixed Word Problems, Analytical Geometry.
Sample Problems:
(Number Theory) Find the least number that when divides by 16, 18 and 20 leaves a remainder 4 in each case, and also completely divisible by 7.
(Geometry) How many cubic centimeters are in the volume of a rectangular prism whose faces have areas 8 sq. cm, 10 sq. cm and 12 sq. cm? Express your answer in simplest radical form.
(Counting and Probability) Seventy-five bingo balls, each with a different positive integer from 1 through 75, are placed in a cage. A random ball is selected, its number is announced, and the ball is returned to the cage. This process occurs a total of 20 times. What is the probability that at least one ball is selected more than once? Express your answer as a decimal to the nearest hundredth.
(Mixed Word Problems) A date is called weird if the number of its month and the number of its day have a greatest common factor of 1. For example, April 15th is weird because the greatest common factor of 4 and 15 is 1. What month has the fewest number of weird days and how many weird days are in that month?
Contents covered in Track A: Logic/Reasoning and Number Bases, Number Theory, Geometry – Pythagorean Theorem, Fractions & Exponents, Arithmetics & Data, Counting and Probability.
Contents covered in Track B: Exponents and Radicals, Functions and Operations, Geometry – Areas, Number Bases and Modular Arithmetic, Set Theory and Mixed Word Problems, Analytical Geometry.
Sample Problems:
(Number Theory) Find the least number that when divides by 16, 18 and 20 leaves a remainder 4 in each case, and also completely divisible by 7.
(Geometry) How many cubic centimeters are in the volume of a rectangular prism whose faces have areas 8 sq. cm, 10 sq. cm and 12 sq. cm? Express your answer in simplest radical form.
(Counting and Probability) Seventy-five bingo balls, each with a different positive integer from 1 through 75, are placed in a cage. A random ball is selected, its number is announced, and the ball is returned to the cage. This process occurs a total of 20 times. What is the probability that at least one ball is selected more than once? Express your answer as a decimal to the nearest hundredth.
(Mixed Word Problems) A date is called weird if the number of its month and the number of its day have a greatest common factor of 1. For example, April 15th is weird because the greatest common factor of 4 and 15 is 1. What month has the fewest number of weird days and how many weird days are in that month?